How Is Geometry Used In Baseball
The Geometry of Shooting
The mathematics of football isn't difficult. Immature players acquire the geometry of the game fifty-fifty earlier they run into the subject in the classroom.
Recall nearly angles and shooting. Here is the dominion: the more of the goal y'all can see when yous shoot, the better your take chances of scoring. Players larn this at seven or 8. They notice that if they overrun the ball in the box, they end up striking the side netting. Ten-year-olds learn to defend by reducing the angles: showing the attacking role player the way out to goal line. Even primary school kids tin calculate the angles for scoring and defending goals.
The rules for shooting are mathematical, even if nosotros don't always notice it. The figure below shows three different shooting positions and the angles between the goal posts.
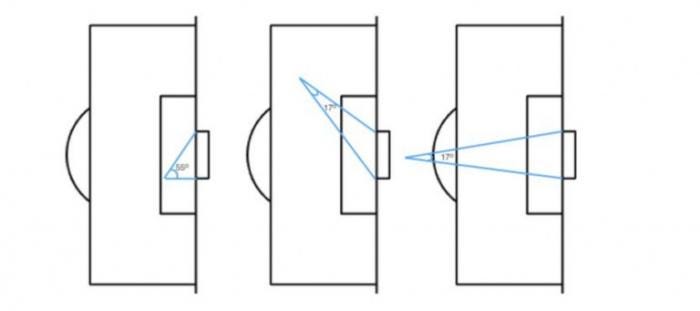
In the left-hand example the angle is 55 degrees, giving a very practiced gamble of a goal from here. In the center and right-hand figures the angles are both 17 degrees, providing much narrower chances.
Football analytics should have what we know about the game and gain insight by looking at information technology more than thoroughly. Nosotros use maths and data to find an edge. Below I bear witness shot success statistics in terms of the angle to the goal mail shown higher up.
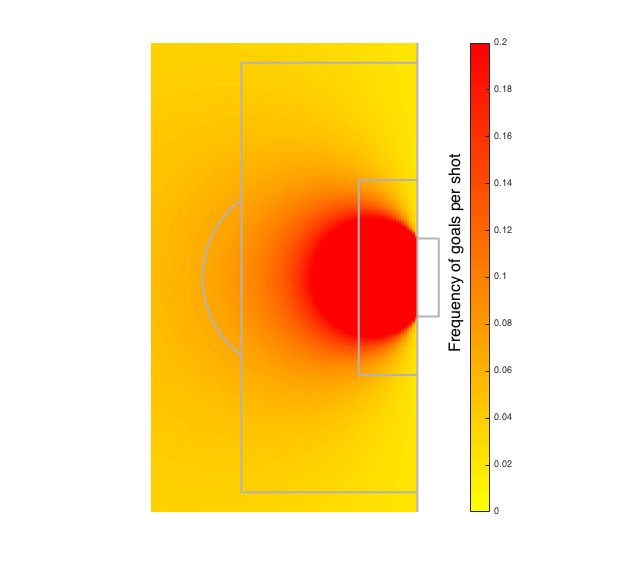
Now nosotros take moved from a training ground discussion with kids, to using Opta's shot data over the last ii seasons. The more cherry-red the colour, the college the probability a shot went in from this position during the past flavor. Shots from the vivid crimson area have at least a twenty% chance of going in. The circle marked past the colour change from yellowish to orange is where the probability of scoring is effectually 5%. Farther out the probability of scoring drops off dramatically.
To summate the probabilities I have fit a statistical model where I use the bending between a line drawn to the goal posts to predict the probability of a goal. This means that I assume that at points on the pitch where the angle is the same, the probability of a goal is the same. For the 55 degree bending in the elevation figure the probability of scoring is simply over 30%. For the 17 degree angle it is simply less than vi%. The larger the angle, the improve the chance.
The analysis to a higher place is the starting point for expected goals models, which we will wait at in depth in this series. For now, nosotros tin take our analysis one footstep further by including distance to goal and altitude to eye of the pitch in our model. Doing this, nosotros go the following picture of the probability of scoring for different points around the box.
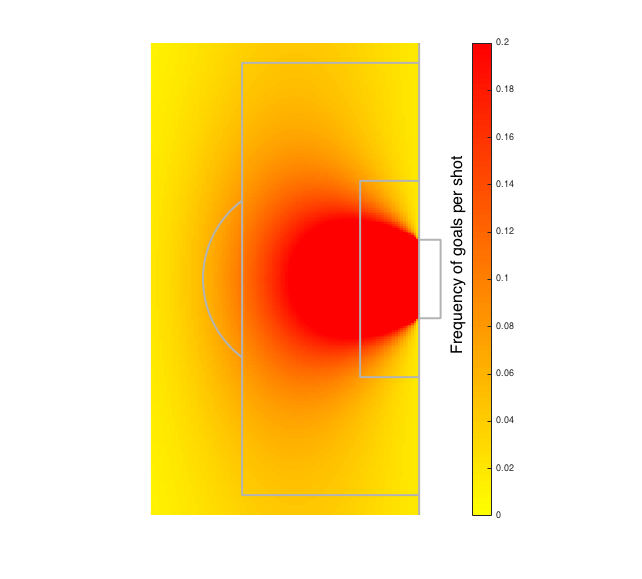
This is a more nuanced, and more authentic, picture show of shooting success. Instead of the circles nosotros found when nosotros looked only at the angle to the posts, we become a sort of squashed out circumvolve. In exercise, this tells us that shooting from a scrap wider out can still upshot in a goal.
Barcelona are specialists in creating chances close to goal with high shot quality. Here are shots for Messi, Neymar and Suarez concluding season. The black circles mark shots that went in.
Messi is the merely of the three attacking players who shoots from further out, and his longer distance efforts tend to exist reasonably key
Real Madrid on the other hand focus on shot volume. Here are shots and goals past Bale, Benzema and Cristiano Ronaldo last season.
Different teams prefer different strategies for shooting, but it is important that all players understand the merchandise-offs involved in having a go from further out and/or from more difficult angles. When Ronaldo scores from exterior the box there is 100% probability we run across it on the friction match highlights. Merely we shouldn't forget that for every i of his long altitude goals he fails to score about 30 times.
Further reading
Ted Knutson has written an excellent article on shooting position, providing a detailed analysis of where to shoot from.
Venezuelan engineer, Cesar Morales, has proposed that the shape of the penalty area should be redrawn to expect more like the squashed circumvolve of shooting success.
Geek box
To calculate the mail service bending, θ, I take the (x,y) co-ordinate of the shot, where x is distance along the edge of the pitch from the goal line and y is the distance from the middle of the pitch. (0,0) is the point on the goal line in the middle of the goal mouth. The angle betwixt two vectors pointing to the goal posts is:
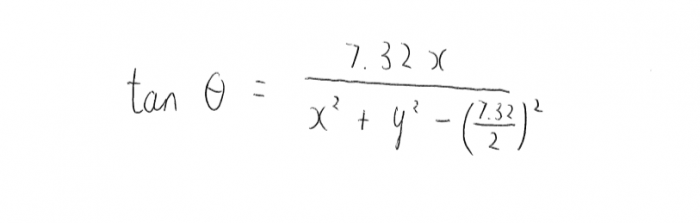
The origins of this equation aren't immediately obvious and it is a fun do in high-school trigonometry to derive it. Hint: 7.32 is the width of the goal!
In order to fit the model to the data I use logistic regression. I fit two models. First I just use the bending and find that the model that best predicts probability of the goal is:
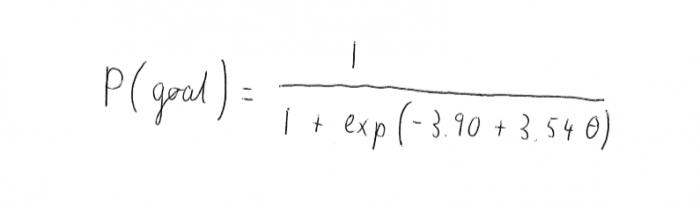
This equation is plotted in the get-go heat map. (there is an error in the in a higher place equation, information technology should be +3.90–3.54theta, the same error appears in the post-obit equations)
Including the distance to the goal line, 10, improves the model fit and I detect that the best model for goal prediction is:
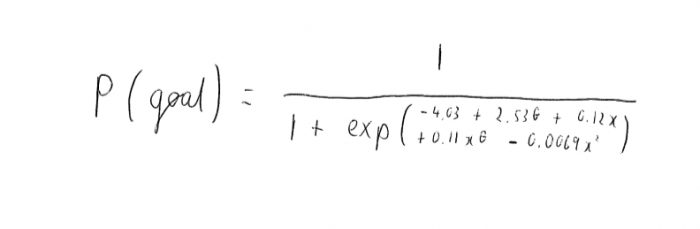
The second heat map shows this equation.
This article originally appeared on Nordic bet.
How Is Geometry Used In Baseball,
Source: https://soccermatics.medium.com/the-geometry-of-shooting-ae7a67fdf760
Posted by: tusseyfalf1986.blogspot.com


0 Response to "How Is Geometry Used In Baseball"
Post a Comment